
N.D. Haasbroek
Nederlandse Commissie voor Geodesie 16, Delft, 1972. 222 pagina's.
ISBN-13: 978 90 6132 023 4. ISBN-10: 90 6132 023 2.
Introduction
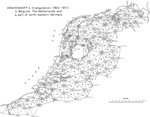
Krayenhoff's triangulation in a part of Belgium, The Netherlands ( with the exception of the province of Limburg ), and a part of northwestern Germany, carried out between 1802 and 1811 and published in his Precis Historique was praised to the skies shortly after its completion also because of the appreciative but rash judgments of Delambre and Van Swinden.
The first who, in 1824-1825, in his letters to Schumacher, Bessel, and Olbers criticized Krayenhoff's work was the great German mathematician C.F. Gauss. To Bessel e.g. he writes: "Krayenhoff hat aus vielen Winkelreihen immer nur diejenigen beibehalten die am besten zu passen schienen, ohne anzugeben wieviel die anderen abweichen".
In the same strain he writes to his pupil and friend Schumacher: "Entweder muss also Herr Krayenhoff seine Ausgleichungen nicht gehörig gemacht haben oder seine Winkelmessungen involvieren versteckter Weise viel grössere Fehler als man nach der Prüfung durch die Dreiecke und die Gyruswinkel erwarten sollte und im letzten Fall ist man berechtigt zu glauben dass die angegebenen Beobachtungswinkel wenigstens parteiisch gewählt sind um diese Schliessung der einzelnen Dreiecke und Tours d'horizon zu erzwingen".
In The Netherlands, Gauss' adverse criticism was borrowed by Verdam; on the pages 206-214 of his "Methode der kleinste quadraten" (Method of the least squares, Groningen, 1850) he reproduces in detail what Gauss had said on the accuracy of the northeastern part of the triangulation network ( the surroundings of Drachten, Leeuwarden, and Dokkum ). In Jordan's "Handbuch der Vermessungskunde" this same part of the network is discussed.
In 1864 appears, also in The Netherlands, the criticism of Kaiser and Cohen Stuart: "De eischen der medewerking aan de ontworpen graadmeting in Midden Europa voor het Koningrijk der Nederlanden". As the title: "Requirements for the cooperation of the Kingdom of The Netherlands in the designed Middle European Triangulation "already suggests, the motive for this criticism was a request of the Prussian general Baeyer whether Krayenhoff's observations could be used for such a triangulation.
Baeyer claimed that, if so, the measurements should be recomputed and suggested that, like in other countries, some army officers should be charged with this work under the supervision of Kaiser. The measurements should be completed with new astronomical measurements. The inaccuracy in length between two far distant points in the adjusted network should not exceed the factor 1 to 20,000. For, such was the reasoning in those days, if the inaccuracy of latitude determination is estimated at about 1/3" ( about 10 metres ), and the distance between two astronomical stations at about 200 km, then the error in length on account of the astronomical determination is about 1 to 20,000.
Apart from his introduction on the pages 4-16 of the booklet, Kaiser has not collaborated with the investigation laid down in the latter part. As the wellknown and elder astronomer he only gave his name to the contents. All the work - and it was a thorough investigation indeed - was done by Cohen Stuart. He concludes that Krayenhofffs measurements should be rejected. His judgment agrees with Gauss' opinion: the far too small closing errors (standard deviation m1) in the angles around a central point, the also very small closing errors in the sum of the angles of the triangles (standard deviation m2) and the often considerable closing errors (standard deviation m3) in the sine equations demonstrate that Krayenhoff made his observations look better than they really are. In reality, according to Cohen Stuart, the standard deviations m1, m2, and m3 should be alike when the observations are independent of each other. By this judgment the sentence on Krayenhofffs triangulation was passed.
After a new but unsuccessful attempt for a triangulation by Stamkart in the years 1865-1881 it has been replaced in The Netherlands by the network of the Rijksdriehoeksmeting. The first order measurements for the network were carried out between 1885 and 1905 by the Rijkscommissie voor Graadmeting en Waterpassing (government commission for Triangulation and Levelling ). They
have a high accuracy as may be found in the publication of the first order triangulation in "Triangulation des Pays Bas". Thanks to the precautions during the measurements and the system of measuring the angles on a station in all combinations, m1, m2, and m3 are about alike as Cohen Stuart made it already his ideal. These results could be attained by much self-control which made the art of measuring a waiting for the most favourable circumstances. At Finsterwolde, e.g., one of the first order points, the two engineers charged with the measurements, remained for six weeks with the result that not even one angle could be measured. In 1888 at only three stations the measurements could be finished. Cohen Stuart should have known, however, that even in his time not one triangulation satisfied these conditions and that also his demands do not hold for the very large English triangulation described in "Account of the Principal Triangulation of the Ordnance Survey of Great Brittain and Ireland (London 1858)" .
Twenty five years later - in 1889 - Van der Plaats returned to the subject of Krayenhoff's triangulation in an excellent paper in the Dutch professional journal "Tijdschrift voor Kadaster en Landmeetkunde" [ 20 ] . Not, as Gauss and Cohen Stuart did, to condemn the triangulation but to take it under protection because the judgment of its opponents "is partial and based upon wrong principles of justice and wrong considerations". In an often emotional manner and certainly not free from a theatrical effect he reacts on Cohen Stuart's judgment "that the measurements are far too inaccurate to be used for the new Middle European Triangulation. It is even not possible, neither to judge Krayenhoff's measurements, nor to recompute them as even his registers are not the unchanged results of mutual independent observations" with the words:
"Let us suppose that (what would not have been impossible) this judgment would have been given in 1818. With fervent indignation the then sixty years old general would have answered to the waylayer of his honour: Judge, yes condemn my geodetic work; an honest judgment is welcome to me and I will answer, give information, and correct my work as much as I can. But don't attack my personality. Are you a stranger in the national history of the past twenty years that you think me capable of such a thing. I have concealed nothing in my documents, nothing added to or withheld from the results of the observations. Go and investigate the publications of others; test my work by theirs". I shall have the opportunity to quote Van der Plaats' work several times. Here follows already such a quotation in which he remarks that "the only effectual means to judge a triangulation is to compare it with a later one with an uncontested higher accuracy".
Up till now this was never done. This study will be an attempt. It can give an answer to the question whether, according to the requirements of 1864, (a relative length error of 1 to 20,000 between two far distant points in the recomputed network) Krayenhoff's measurements could be used or had to be rejected. Van der Plaats was convinced that they could be used, notwithstanding the imperfection of the triangulation which he admits. For Krayenhoff's rehabilitation as geodesist according to Van der Plaats the following lines of poetry might then be used as an introduction to an eventual new (third) edition of his Precis Historique. They are borrowed from Racine's tragedy Brittannicus (second act, third scene) and they run:
"J'ose dire pourtant que je n'ai mérité
Ni cet excès d'honneur, ni cette indignité".
Contents
1. Introduction 9
2. Krayenhoff's biography 12
3. The motive for the triangulation 14
I. Geodetic part of the triangulation
4. General survey of the triangulation 16
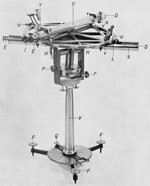
5. Description of the instruments used 20
6. Execution of the angular measurements 24
7. Chronological order in which the stations were visited and survey of the number of angles and series measured there 31
8. Accuracy of the angular measurement 37
9. Influence of the eccentricity of the lower telescope on the result of the angular measurements 40
10. Reduction of the measured space angles to the horizon 42
11. Reduction of the measured angles to centre 43
12. Reduction of the spherical angles, reduced to horizon and centre, to angles between the chords on the sphere 51
13. Conditions the angles of the triangulation network have to comply with 56
14. Analysis of the closing errors in the angles around the central points 84
15. Analysis of the closing errors in the triangles 87
16. Analysis of the closing errors in the side equations 110
17. Consideration on the rejection of series measured in the triangulation 112
18. Krayenhoff's computation of his triangulation network and his efforts to make it a closing mathematical figure 118
19. Adjustment of the spherical angles of the triangulation network according to the method of the least squares 129
20. Provisional adaptation of the adjusted network to the points Rhenen and Gorinchem of the R.D.-triangulation 131
21. Final adaptation of Krayenhofft s adjusted triangulation to 65 identical points of the R.D.-network 135
22. Comparison between the side lengths in tableau I11 of the Precis Historique and those found from the adjustment according to the method of the least squares 140
23. Comparison of the angles and sides (chords) of the adjusted network with the results of the R.D. 143
24. Final consideration on the geodetic part of the triangulation 154
II. Astronomical part of the triangulation
25. Introduction 156
26. Determination of the latitude in Amsterdam (station No. 40) 157
27. Determination of the latitude at Jever (station No. 102) 163
28. Determination of astronomical azimuths. General considerations and results of the measurement of the azimuth Amsterdam-Utrecht 167
29. Measurement and computation of the azimuth Jever-Varel 178
30. Instrumental errors, affecting the accuracy of the determination of azimuths 186
31. Determination of standard deviations in azimuths 188
32. Survey of the geographical coordinates φ and λ of all the points of the triangulation network and the azimuths of all the sides and, for the common points and sides, a comparison with the R.D.-results 192
33. Conclusions 214
References 219