Prof.dr.ir. P.J.G. Teunissen
Op 13 januari 2010 overleed het langjarig lid van de Nederlandse Commissie voor Geodesie (NCG) prof.ir. J.E Alberda. Jouke Alberda was van 1980 tot 1997 lid van de Commissie en hij bekleedde van 1980 tot 1992 de functie van secretaris. In deze functie kreeg hij te maken met de overgang van de NCG naar de Koninklijke Nederlandse Akademie van Wetenschappen (KNAW). Deze overgang op 1 januari 1990 heeft hij op een uitstekende wijze voorbereid en begeleid. Alberda is ook lid geweest van de Werkgroep Geschiedenis der Geodesie van de NCG en haar voorganger de Rijkscommissie voor Geodesie.
Jouke Alberda werd in 1926 in Oss geboren, volgde daar de HBS en ging vervolgens naar de MTS (huidige HTS). Na zijn verblijf in Nederlands-Indië, begon hij in 1949 aan zijn studie geodesie aan de Technische Hogeschool te Delft, alwaar hij in 1954 als een van de eerste studenten van deze nieuwe opleiding afstudeerde. In 1970 werd Alberda lector bij de werkeenheid Mathematische Geodesie en Landmeetkunde van prof.dr.ir. W. Baarda (1917 - 2005). In 1980 werd de rang van lector opgeheven en werd Alberda hoogleraar. Zijn wetenschappelijk werk wist Alberda te combineren met verschillende bestuurlijke functies. Bovendien was hij actief in het (internationale) geodetische verenigingsleven [1].
Jouke Alberda werd altijd geroemd om zijn talenkennis. Maar naast zijn talenknobbel had hij zeker ook een wiskundeknobbel, die hem zeer goed van pas kwam in de pioniersjaren waarin de Delftse theorie tot bloei kwam. Van zijn wetenschappelijk werk wil ik hier nader ingaan op zijn bijdragen aan de Europese waterpassing, zijn besliskundige benadering van de geodetische kwaliteitsbeheersing en zijn precisieanalyse van netwerken leidend tot zijn eigen originele constructie van de 'kunstmatrix' H.
Waterpassingen
Alberda heeft in de jaren 1960 een belangrijke rol gespeeld bij de realisering van het Europese hoogtesysteem [2], [3]. Samen met zijn collegae van het Laboratorium voor Geodetische Rekentechniek (LGR) heeft hij de berekening, de analyse en de validatie van het Europese waterpasnetwerk uitgevoerd. Door zijn gedegen wiskundige kennis en zijn nauwe samenwerking met prof. Baarda was hij al vroegtijdig een expert in de Delftse vereffenings- en toetsingstheorie [4]. Hij was dan ook een van de eersten die deze, toen nog jonge theorie succesvol wist toe te passen, daarbij overtuigend demonstrerend waartoe de theorie in staat was.
De vereffening en de toetsing van het Europese netwerk zijn door Alberda en zijn collegae op een van de eerste Nederlandse computers, de Zebra, uitgevoerd. De Zebra (Zeer eenvoudige binaire rekenautomaat) was een Nederlands ontwerp en het was de eerste computer van de TH Delft. De netwerkvereffening is volgens de principes van prof. J.M. Tienstra's methode van fasevereffening uitgevoerd. Deze op het eerste standaardvraagstuk gebaseerde vereffeningsmethode is numeriek efficiënt en zeer geschikt voor waterpasnetwerken. Dat numerieke efficiëntie essentieel was, moge duidelijk zijn als men bedenkt dat het inverteren van een 30 bij 30 matrix met de Zebra 63 minuten kostte!
Met de succesvolle afronding van dit project stond het LGR internationaal op de kaart. Een overzicht van de resultaten werd in 1960 gepubliceerd in Bulletin Géodésique [2] en het eindrapport verscheen in 1963 in de Publications on Geodesy van de Rijkscommissie voor Geodesie [3]. Het was, zoals Alberda later zelf bescheiden zou zeggen, "een fraaie gelegenheid om Delftse ideeën toe te passen: vereffening in fasen volgens Tienstra en statistische toetsingen volgens Baarda". Het zou ook de start zijn van de Delftse deelname aan andere grote internationale onderzoeksprojecten.
Besliskunde
De Delftse theorie van kwaliteitsbeheersing - oorspronkelijk door Baarda en zijn medewerkers ontwikkeld voor geodetische netwerken - werd al gauw ook in andere geodetische disciplines toegepast. Deze verbreding maakte het nodig scherper dan voorheen de maatschappelijke (en soms wetenschappelijke) doelstellingen van geodetische werkwijzen te formuleren en te kwantificeren. Door deze werkwijzen in een besliskundig kader te plaatsen [5 - 7], is het Alberda gelukt scherper aandacht te geven aan de consequenties van geodetische beslissingen, daarmee tevens duidelijk makend welke uiteenlopende factoren daarbij een rol spelen. Dat de toepassing van besliskundige methoden uiteindelijk toch geen grote ingang hebben gevonden, is voor een belangrijk deel te wijten aan de praktische moeilijkheid om geschikte kostenfuncties op te stellen. Niettemin heeft het hanteren van de besliskundige gedachtegang ertoe geleid dat de Delftse theorie van kwaliteitsbeheersing in een ruimer kader geplaatst kon worden.
Netwerkprecisie
Elke geodeet weet dat de namen van Tienstra en Baarda verbonden zijn aan de precisietheorie van netwerken. Dat Alberda ook een cruciale rol in de ontwikkeling van deze theorie heeft gespeeld, is echter veel minder bekend [8 - 10]. Zijn bijdrage betreft vooral de zoektocht naar een kunstmatige covariantiematrix (de 'kunstmatrix' H) om de precisie van coördinaten in geodetische netwerken te kunnen beschrijven. Deze kunstmatrix zou dan enerzijds gebruikt kunnen worden als vervangingsmatrix voor het beschrijven van de coördinatenprecisie van gegeven (hogere-orde)punten en anderzijds als criteriummatrix voor het toetsen van de precisie van nieuw ontworpen vrije netwerken.
Om tot een geschikte vervangingsmatrix te komen, zou deze een eenvoudige structuur moeten hebben en tegelijk voldoende moeten lijken op de echte covariante matrix van een goed netwerk. Mede gebaseerd op de HTW-56 (Handboek Technische Werkzaamheden 1956) heeft Alberda een kunstmatrix ontworpen waarin de standaardellipsen van alle punten cirkelvormig waren met gelijke straal en de relatieve standaardellipsen cirkelvormig waren met een straal afhankelijk van de afstand tussen de betrokken punten. Voor twee netwerkpunten i en j werd de structuur van de kunstmatrix dus gegeven door de 4 bij 4 deelmatrix
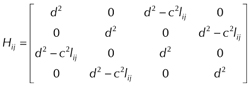
waarin c2 en d2 nog te kiezen parameters zijn en lij de afstand is tussen de punten i en j. Alberda heeft toen laten zien dat het precisieverloop van de geschrankte vorm van deze H-matrix mooi overeenkwam met dat van echte netwerken. Het patroon van covariantie-isolijnen vertoonde dezelfde structurele eigenschappen als die hij al eerder empirisch in geodetische netwerken had gevonden. Daarmee was de bekende Delftse kunstmatrix een feit.
Hoewel Alberda en Baarda in hun zoektocht naar H verschillende wegen hebben bewandeld, is het bevredigend dat beiden tot dezelfde conclusies en resultaten zijn gekomen. Het is zoals Baarda schrijft [12]: "the differences in argumentation will lead to a clarification of the line of thought". Een mooi overzicht geeft Alberda in 'Planning and Optimization of Networks: Some General Considerations', verschenen in het Italiaanse tijdschrift Bollettino di Geodesia e Scienze Affini [9].
Als eerbetoon en blijvende herinnering aan een bijzondere geodeet, stel ik voor om ook de naam van Alberda te verbinden aan de Delftse precisietheorie, door de 'kunstmatrix' H vanaf nu de Alberda-Baarda-matrix te noemen (in kort de AB-matrix).
| Verwijzingen | |
| [1] | Bogaerts Th., H. Quee (2010): Prof.ir. J.E. Alberda (1926-2010) - landmeter, bruggenbouwer, gentleman. Geo-Info, 2010-3, p.46. |
| [2] | Alberda J.E., B.G.K. Krijger, E.F. Meerdink (1960): The adjustment of UELN as executed at Delft. Bulletin Geodesique, 34(1), 41-53. |
| [3] | Alberda J.E. (1963): Report on the adjustment of the United European Levelling Net and related computations. Netherlands Geodetic Commission. Publications on Geodesy, New Series, Vol. 1, No. 2. |
| [4] | Baarda W., J.E. Alberda (1962): The Connection of Geodetic Adjustment Procedures with Methods of Mathematical Statistics. Bulletin Geodesique, 36(4), 325-345. |
| [5] | Alberda J.E. (1965): Elementaire aspecten van de besliskunde. LGR rapport R40, 35p. |
| [6] | Alberda J.E. (1966): On the Importance of Decision Theory for Geodesists. Proceedings 2nd International Symposium on Geodetic Calculations, Brussels, 121-142. |
| [7] | Alberda J.E. (1968): Decision Making and Surveying. Paper presented at 12th International Congress of Surveyors. 8p. |
| [8] | Alberda J.E. (1974): Aspects of Large Leveling Nets. The Canadian Surveyor, 28(5), 643-652. |
| [9] | Alberda J.E. (1974): Planning and Optimization of Networks: Some General Considerations. Bollettino di Geodesia e Scienze Affini, 33, 209-240. |
| [10] | Alberda J.E. (1976): Quality Control in Surveying. Chartered Surveyor Land Hydrographic and Minerals Quarterly Vol. 4, No. 2, 1976/77. |
| [11] | Alberda J.E. (1982): A Note on the Simplest Substitute Matrix. In het Baarda Gedenkboek 'Daar heb ik veertig jaar over nagedacht |